OpenSearch 2.19 introduces reciprocal rank fusion (RRF), a new feature in the Neural Search plugin that enhances hybrid search. RRF merges ranked results from multiple query sources, such as neural search, k-NN, and Boolean queries, into a single relevance-optimized list. By prioritizing documents that consistently rank highly across different sources, RRF improves search relevance without relying on traditional score normalization techniques.
Why use RRF for hybrid search?
RRF is particularly useful for aggregating ranked results from diverse query methods. Unlike traditional normalization techniques such as min-max or L2 normalization, which adjust scores to a shared scale, RRF uses a rank-based aggregation strategy. This approach delivers the following advantages over score-based methods, enhancing stability and relevance in hybrid search.
Stability across varying score distributions
Traditional normalization techniques like min-max adjust scores from different query methods so that they fit within a standardized scale. However, when merging results from different query methods, variations in score distributions can lead to unbalanced rankings. One method’s scoring pattern may dominate, reducing search quality. L2 normalization scales scores proportionally but remains influenced by score distributions within individual queries. RRF avoids these issues by focusing exclusively on rank positions, ensuring consistent treatment of results across disparate data sources.
Resistance to outliers
Min-max and L2 normalization are sensitive to outliers, meaning extreme scores can disproportionately impact final rankings. Because RRF aggregates rankings rather than scores, it prevents anomalous values from distorting relevance.
Consistency in relevance ranking
L2 normalization aligns scores to a common scale but lacks a mechanism for prioritizing documents that appear across multiple queries. RRF excels at this by favoring items that rank highly across diverse query methods, ensuring more reliable relevance ranking.
Practical applications of RRF
RRF is particularly effective in search scenarios where datasets present specific challenges.
Handling score variability across query methods
Different search methods—such as BM25, neural search, and k-NN—produce scores on incompatible scales. Techniques like L2 or min-max normalization attempt to standardize these scores but can lead to suboptimal rankings. RRF sidesteps this issue by emphasizing rank consistency rather than absolute score alignment.
Example: In multimodal search pipelines, where text-based queries produce a wide range of scores while visual features generate a narrower range, RRF ensures that smaller-scale signals are not overshadowed.
Enhancing e-commerce search with sparse behavioral signals
E-commerce datasets often contain sparse behavioral signals, such as user clicks or purchases, which can be difficult to incorporate into search rankings. Rank-based aggregation helps highlight relevant products even when engagement data is limited.
Example: When merging behavioral data with metadata, RRF ensures that niche products with high semantic or metadata relevance remain visible, whereas min-max and L2 normalization may struggle with sparse signals.
Managing noisy or outlier-prone data
Datasets with high variance or frequent outliers—such as scientific research or log data—pose challenges for score-based methods like min-max or L2. RRF prevents outliers from distorting search results by focusing on rank rather than score.
Example: In scientific datasets, metadata from top-tier journals often skews scores. RRF integrates these results without overemphasizing outliers, leading to more balanced rankings.
Supporting dynamic or evolving data
Rapidly changing datasets, such as streaming logs, require frequent recalibration for L2 and min-max normalization, which can introduce instability or latency. RRF maintains stable rankings by aggregating based on static rank positions.
Example: In log search pipelines, RRF consistently prioritizes frequently occurring patterns, even as scoring distributions shift over time.
Comparing RRF with score-based methods
The following table compares two hybrid search approaches using the same query: a standard hybrid search pipeline and an RRF-based hybrid search pipeline. We selected the top three and bottom three results for comparison. Notice that RRF provides more consistent scores across documents because it ranks them based on the relative rank (position) of a document within each query result rather than on raw scores.
min_max and arithmetic_mean |
RRF |
|---|---|
| 0.5 | 0.01639 |
| 0.29481 | 0.01613 |
| 0.28132 | 0.01587 |
| 0.01396 | 0.01471 |
| 0.00386 | 0.01449 |
| 0.0005 | 0.01429 |
How RRF works
RRF ranks documents by performing the following steps:
- Sort documents by score: Each query method sorts documents by score on every shard.
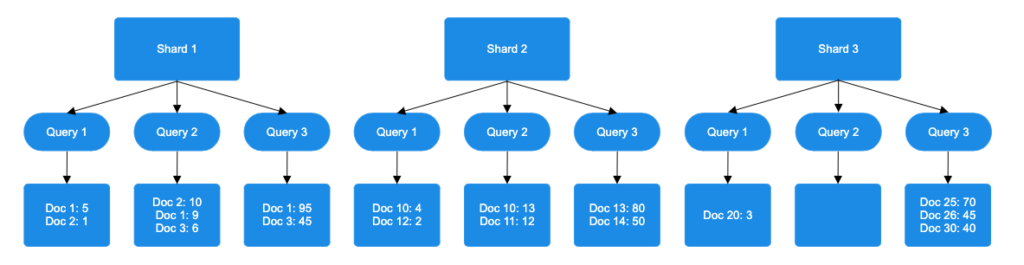
- Assign rank positions: Documents are ranked based on score for each query.
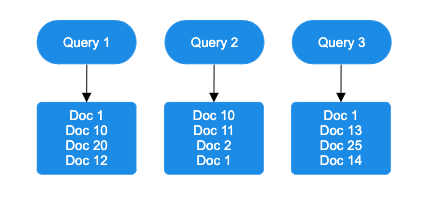
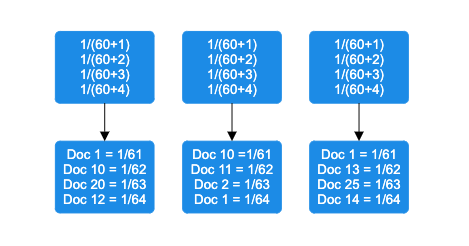
- Apply the RRF formula: The RRF score is computed using the following formula:
rankScore(document_i) = sum((1/(k + query_1_rank), (1/(k + query_2_rank), ..., (1/(k + query_j_rank)))In this formula, k is a rank constant, and query_j_rank represents the ranking of a document in a particular query method. The example in the following diagram applies this formula using the default rank constant of 60.
- Add rank contributions: Rank calculations are combined, and documents are sorted by decreasing rank score.
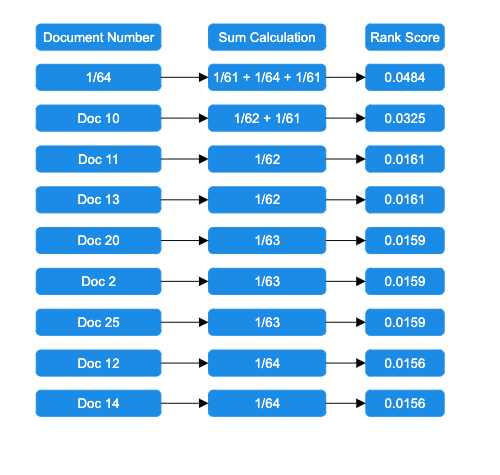
- Return the top results: The highest-ranked documents are retrieved based on the query size.
How to use RRF
To use RRF, create a search pipeline and specify rrf as the technique:
PUT /_search/pipeline/rrf-pipeline
{
"description": "Post processor for hybrid RRF search",
"phase_results_processors": [
{
"score-ranker-processor": {
"combination": {
"technique": "rrf"
}
}
}
]
}
You can also specify the rank constant as part of the pipeline; the rank constant must be 1 or greater. Larger rank constants make the scores more uniform, reducing the impact of top-ranked items. Smaller rank constants create steeper differences between ranks, giving much more weight to top-ranked items. By default, the rank constant is set to 60:
PUT /_search/pipeline/rrf-pipeline
{
"description": "Post processor for hybrid RRF search",
"phase_results_processors": [
{
"score-ranker-processor": {
"combination": {
"technique": "rrf",
"rank_constant": 40
}
}
}
]
}
Next, create a hybrid query and apply the pipeline to it:
POST my_index/_search?search_pipeline=rrf-pipeline
{
"query": {
"hybrid": [
{}, // First Query
{}, // Second Query
... // Other Queries
]
}
}
Benchmarking RRF performance
Benchmark experiments were conducted using an OpenSearch cluster consisting of a single r6g.8xlarge instance as the coordinator node, along with three r6g.8xlarge instances as data nodes. To assess RRF’s performance comprehensively, we measured three key metrics across six distinct datasets. For information about the datasets used, see Datasets.
Search relevance was quantified using the industry-standard Normalized Discounted Cumulative Gain at rank 10 (NDCG@10). We also tracked system performance using search latency measurements and monitored CPU utilization to analyze resource consumption during the experiments. This setup provided a strong foundation for evaluating both search quality and operational efficiency.
NDCG@10
The following table compares the NDCG@10 scores across different search methods (BM25, Neural, Hybrid, and Hybrid with RRF) for various datasets. The Percent difference column shows the relative performance change between the Hybrid and Hybrid with RRF approaches.
| BM25 | Neural | Hybrid | Hybrid with RRF | Percent difference | |
|---|---|---|---|---|---|
| NFCorpus | 0.3065 | 0.2174 | 0.3076 | 0.2977 | 3.22% |
| ArguAna | 0.4258 | 0.4239 | 0.4507 | 0.4476 | 0.69% |
| FIQA | 0.2389 | 0.2004 | 0.2693 | 0.2474 | 8.13% |
| Trec-Covid | 0.6087 | 0.2718 | 0.5905 | 0.5877 | 0.47% |
| SciDocs | 0.155 | 0.1075 | 0.1602 | 0.1525 | 4.81% |
| Quora | 0.7424 | 0.8256 | 0.8452 | 0.796 | 5.82% |
| Average: | 3.86% |
Search latency
The following table presents search latency measurements in milliseconds at different percentiles (p50, p90, and p99) for both the Hybrid and RRF approaches. The Percent difference columns show the relative performance impact between these methods.
| p50 | p90 | p99 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hybrid | RRF | Percent difference | Hybrid | RRF | Percent difference | Hybrid | RRF | Percent difference | |
| NFCorpus | 71 | 67.5 | 4.93% | 95 | 89.9 | 5.37% | 112.84 | 109.56 | 2.91% |
| ArguAna | 390.5 | 390 | 0.13% | 423.5 | 424 | -0.12% | 459.475 | 458.5 | 0.21% |
| FIQA | 109 | 105.25 | 3.44% | 139.65 | 137.5 | 1.54% | 165.76 | 160.79 | 3.00% |
| Trec-Covid | 165.5 | 159.75 | 3.47% | 209.5 | 203.6 | 2.82% | 240.73 | 237.78 | 1.23% |
| SciDocs | 103 | 103.5 | -0.49% | 126.5 | 126.05 | 0.36% | 156.02 | 159.015 | -1.92% |
| Quora | 167 | 170 | -1.80% | 209.5 | 212.55 | -1.46% | 264.5 | 266.51 | -0.76% |
| Average: | 1.62% | Average: | 1.42% | Average: | 0.78% | ||||
CPU utilization
The following table shows CPU utilization measurements on the coordinator node, comparing the Hybrid and RRF approaches. The Percent difference column indicates the relative change in CPU usage between the two methods.
| Hybrid | RRF | Percent difference | |
|---|---|---|---|
| NFCorpus | 0.783% | 0.838% | 0.055% |
| ArguAna | 0.844% | 0.853% | 0.008% |
| FIQA | 0.835% | 0.851% | 0.016% |
| Trec-Covid | 1.406% | 0.979% | -0.427% |
| SciDocs | 0.745% | 0.873% | 0.128% |
| Quora | 1.054% | 1.076% | 0.022% |
| Average: | -0.033% |
Conclusions
Our benchmark experiments highlight the following advantages and trade-offs of RRF compared to conventional hybrid search approaches:
- Search quality (measured using NDCG@10 across six datasets):
- RRF scores 3.86% lower than traditional score-based methods.
- Latency improvements:
- RRF consistently outperforms traditional normalization techniques, as shown in the following table.
| Latency percentile | Percent improvement |
|---|---|
| p50 | 1.62% |
| p90 | 1.42% |
| p99 | 0.78% |
- Resource efficiency:
- Similar CPU usage on the coordinator node
- More efficient resource distribution across all node types
RRF offers a compelling alternative to traditional hybrid search methods, delivering improved performance and resource efficiency with minimal impact on search quality. It also provides significant latency improvements, making it particularly suitable for high-throughput search applications.
What’s next?
Our roadmap includes several important enhancements to RRF:
- Customizable weights: We plan to implement weight support similar to score-based ranking techniques, allowing more nuanced control over the ranking algorithm. For more information, see this issue.
- Better handling of missing items: Currently, missing items default to a score of 0.0, but this may not be optimal for all use cases. We’re exploring multiple approaches for handling missing items, such as configurable default values, using
max_rank + 1for missing items, or completely ignoring missing items in calculations. For more information, see this issue.
We are also expanding OpenSearch’s hybrid search capabilities beyond RRF by planning the following improvements to our normalization framework:
- Z-score normalization: Adds the popular z-score normalization technique. For more information, see this pull request.
- Custom normalization functions: Enables you to define your own normalization logic and allows fine-tuning of search result rankings. For more information, see this issue.
These improvements will provide more control over search result ranking while ensuring reliable and consistent hybrid search outcomes. Stay tuned for more information!
References
- [RFC] Design for Incorporating Reciprocal Rank Fusion into Neural Search
- BEIR benchmarking for Information Retrieval
- Reciprocal Rank Fusion outperforms Condorcet and individual Rank Learning Methods
- Risk-Reward Trade-offs in Rank Fusion
- The ABCs of semantic search in OpenSearch: Architectures, benchmarks, and combination strategies
- Improve search relevance with hybrid search, generally available in OpenSearch 2.10
- [RFC] High Level Approach and Design For Normalization and Score Combination